Introduction
Many years ago, when I was first getting into privacy and security, I wanted to see how long passwords should be in order to be secure from brute forcing. There are plenty of password strength testers already, but I wasn’t sure if they accounted for the increase of cracking speeds over time. Then, the idea came to me: What is the maximum speed for a password cracker?
The Planck Cruncher
The Planck Cruncher is a theoretical supercomputer, designed to crack passwords as fast as the laws of physics will allow. Here is how it is constructed:
Imagine a little computer that can fit in the smallest possible space in the universe: a cubic Planck length. This little computer is able to test one password every Planck time, the shortest possible unit of time. Now, fill every cubic Planck length in the observable universe with these little computers, all testing passwords at the same time, and you have constructed the Planck Cruncher!
I should note here: of course this is impossible to create. This is just a fun idea I had, to test the theoretical security of passwords. Don’t take it too seriously.
How fast is it?
First, you need to calculate how many of those little computers can fit inside the observable universe.
The diameter of the observable universe is estimated to be 8.8×10^26 meters in diameter. To calculate the cubic volume of the observable universe, you can use the equation for the volume of a sphere: 4/3*πr^3
A sphere 8.8×10^26 meters in diameter has a radius of 4.4×10^26 meters. Substitute that into the equation to get 4/3*π*(4.4×10^26)^3 which equals 3.6×10^80 cubic meters in volume.
A Planck length is approximately equal to 1.616255×10^(-35) meters. That means a cubic Planck length would have an area of 4.222111×10^(-105) cubic meters.
Divide the volume of the observable universe by the area of a cubic Planck length, and you get how many little computers make up the Planck cruncher: (3.6×10^80)/(4.222111×10^(-105)) which is approximately 8.52654×10^184 little computers. This is the exact number (rounded up):
85265403964983393378336097748259105456962168924502458604238495861430455049618543899011655543873668882698725826961915496774007125819288029139925501721769039231796606010595173836026575332
Next, you have to find out how many Planck times are in a second.
A Planck time is approximately equal to 5.391247×10^(−44) seconds. To find how many Planck times are in a second, you simply take the inverse of that to get: 1/(5.391247×10^(−44)) which is approximately equal to 1.854858×10^43 Planck times in a second.
If you multiply the number of little computers in the Planck Cruncher by the number of Planck times in a second, you find out how many passwords the Planck Cruncher can test every second: (8.52654×10^184)*(1.854858×10^43) is approximately 1.581553×10^228 passwords tested every second. The exact number is below (rounded up):
1581552541832778082294061053931661922686201706664570527082852925518538754570483301896790400140703419500140242637035837845567215262429787192831741927642510892782256238873773986538301349050212882962091805863577761872814550820473182
The complete equation is this: 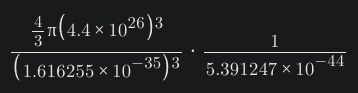
How secure are passwords against it?
Since you know how many passwords the Planck Cruncher can test in a second, you can calculate how secure a password must be to fend it off for, say, 100 years.
There are 95 printable characters on a standard QWERTY keyboard. If you make each character of your password a randomly selected character from the 95 printable characters, you can calculate the number of possible combinations for your password using the equation 95^length where length is the length of your password. I will refer to this as the “complexity” of the password.
With that, you can calculate the bits of entropy of the password by using the equation log2(combinations) where combinations is number of possible combinations for your password. For simplicity, I will be referring to the strength of passwords by their bits of entropy. The unit used to represent entropy is the shannon unit, denoted as “Sh”.
To calculate how many seconds it would take to crack a password, you divide the password complexity by the speed of the Planck cruncher. For example:
An 8 character password has a complexity of 95^8, or approximately 6.6342×10^15. That password has an entropy of log2(6.6342×10^15), or approximately 52.56 Sh. To crack the password, assuming it was the very last password tested, the Planck cruncher would take 4.1947×10^(-213) seconds. That is orders of magnitude shorter than a Planck time itself.
So, how many bits of entropy is secure against the Planck Cruncher? If you wanted a password that is strong enough to keep the Planck Cruncher at bay for 100 years, the password would need an entropy of approximately 789.66 Sh. The password would be 121 characters in length (rounded up).
A passphrase with the same entropy (assuming 7,776 words are in the wordlist, from the EFF Large Wordlist for Passphrases) would have 62 words (rounded up).
Conclusion
Obviously if the the universe is (literally) against you, you have bigger problems than a password protecting your sensitive data. This was just a fun thought experiment to see what the upper limit of password cracking is. It’s interesting to see how a 1024 bit key would be resistant against even the fastest theoretical supercomputer for over a vigintillion years (assuming it has no other weaknesses). I hope you had as much fun reading this as I did writing it. Be sure to use strong passwords, and use a password manager.


Why not both?
You don’t need to do either. Qbits are still bounded by the laws of computation, and the planck supercomputers as described are already perfect computers with infinite bits since they can check a password of any length in a single Planck second of operation. There’s no speed advantage when going from an infinite number of things with unique states to a single thing with infinite states.